17387번: 선분 교차 2
첫째 줄에 L1의 양 끝 점 x1, y1, x2, y2가, 둘째 줄에 L2의 양 끝 점 x3, y3, x4, y4가 주어진다.
www.acmicpc.net
선분 교차 알고리즘
계산 기하학 알고리즘 중 선분 교차 알고리즘을 공부했다.
1. 문제 해결 아이디어
먼저 두 선분이 교차하는 경우를 알아보자


l1선분의 p1, p2벡터에서 l2선분의 p1으로의 방향과
p1, p2벡터에서 l2선분의 p2로의 방향이 서로 다르다면(한 점이 선분에 포함된 경우 포함) 반드시 두 선분은 교차한다.
두 선분의 직선의 방정식을 구해서 교차하는 한 점을 구하면 선분이 교차하는지 알 수 있지 않을까요?
알 수 없다
아래 두 선분을 보자
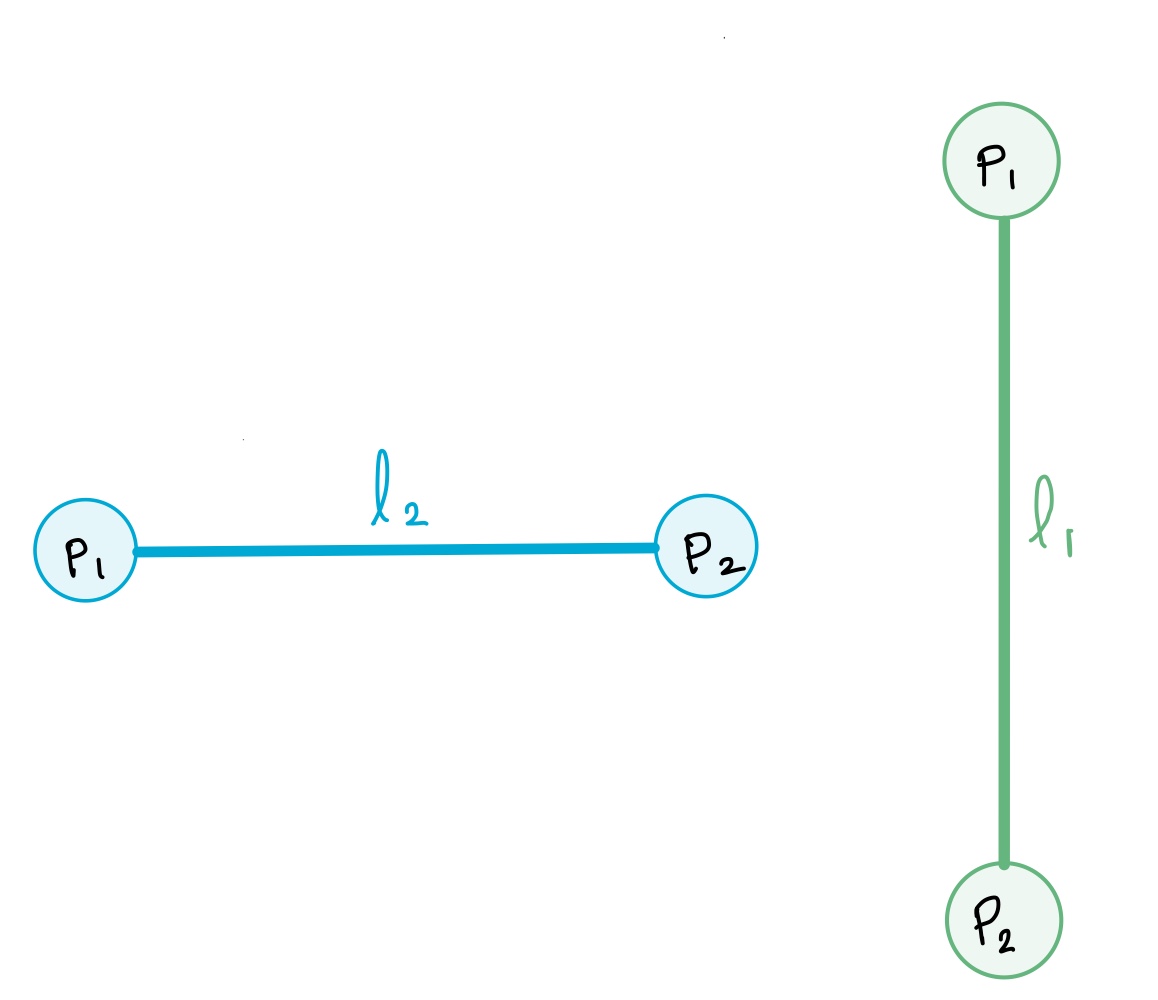
l2선분을 직선으로 만들면 l1과 교차하게된다.
하지만 l1과 l2 선분은 교차하지 않기 때문에 직선의 방정식으로는 문제를 해결할 수 없다.
그럼 선분이 만나지 않는다는건 어떻게 증명하는가?

l1에서 l2의 p1으로 가는 방향과 p2로 가는 방향이 동일하다면 선분은 교차하지 않는다.
이제 두 직선이 서로 일직선 상에 있는 경우를 알아보자

먼저 선분에서 x가 더 작은 점을 p1으로 정렬하자.
두 직선이 일직선에 있을 때 서로 겹칠 수도 있고, 겹치지 않을 수도 있다.
겹치는 경우는 l2의 p1이 l1의 p2보다 작고 l1의 p1이 l2의 p2보다 작다면 겹친다는 의미이다.
위 조건에 해당하지 않는게 겹치지 않고 서로 일직선 상에 있는 경우이다.
2. 코드
- long long 자료형이 필요하다
- 선분을 이루는 두 점을 정렬하기 위해서 <= 연산자를 오버로딩 해주었다. (x가 더 작으면 true)
- CCW는 determinant를 통해서도 똑같이 구할 수 있다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
|
#include <iostream>
using namespace std;
struct P{
long long x, y;
bool operator<=(P const &p1) {
if(x == p1.x){
return y <= p1.y;
}
return x <= p1.x;
}
};
struct Line{
P p1, p2;
};
Line line[2];
int CCW(const P &p1, const P &p2, const P &p3){
long long res = (p1.x*p2.y + p2.x*p3.y + p3.x*p1.y) - \
(p2.x*p1.y + p3.x*p2.y + p1.x*p3.y);
// 행렬식을 통해서 구하기
// int determinant = (p2.x*p3.y - p2.y*p3.x) - \
// (p1.x*p3.y - p1.y*p3.x) + \
// (p1.x*p2.y - p1.y*p2.x);
if(res > 0) return 1; //반시계
else if(res < 0) return -1; //시계
else return 0;
}
bool isline_intersect(Line& l1, Line &l2){
int std1, std2;
std1 = CCW(l1.p1, l1.p2, l2.p1) * CCW(l1.p1, l1.p2, l2.p2);
std2 = CCW(l2.p1, l2.p2, l1.p1) * CCW(l2.p1, l2.p2, l1.p2);
if(std1 <= 0 && std2 <= 0){
if(std1 == 0 && std2 == 0){ //선분이 일직선인 경우
if(l1.p2 <= l1.p1) swap(l1.p1, l1.p2);
if(l2.p2 <= l2.p1) swap(l2.p1, l2.p2);
return l1.p1 <= l2.p2 && l2.p1 <= l1.p2;
}
else return true; //일직선이 아니면 교차함
}
else return false; //CCW가 같은 방향이 있으면
}
void solve(){
if(isline_intersect(line[0], line[1])){
cout << 1;
}
else cout << 0;
}
void input(){
long long x1, x2, y1, y2;
P p1, p2;
for(int i = 0 ; i < 2; i++){
cin >> p1.x >> p1.y >> p2.x >> p2.y;
line[i].p1 = p1;
line[i].p2 = p2;
}
}
int main(){
input();
solve();
return 0;
}
|
cs |
나중에 코드를 다듬어서 class template으로 만들어서 올릴 예정이다
다음은 convex hull !!
'Algorithm > BOJ' 카테고리의 다른 글
| [백준 6543] 그래프의 싱크 C++ (2) | 2021.06.14 |
|---|---|
| [백준 1708] 볼록 껍질 C++ (0) | 2021.06.13 |
| [백준 2150] Strongly Connected Component C++ (0) | 2021.06.10 |
| [백준 1600] 말이 되고픈 원숭이 C++ (0) | 2021.06.09 |
| [백준 8980] 택배 C++ (0) | 2021.06.09 |
![[백준 17387] 선분 교차 2 C++](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2Fb1LZep%2Fbtq64yDGf6Y%2FGnDwhfbEzSYouUA32wpHo1%2Fimg.png)