1309번: 동물원
첫째 줄에 우리의 크기 N(1≤N≤100,000)이 주어진다.
www.acmicpc.net
다이나믹 프로그래밍 기초
1. 문제풀이 아이디어
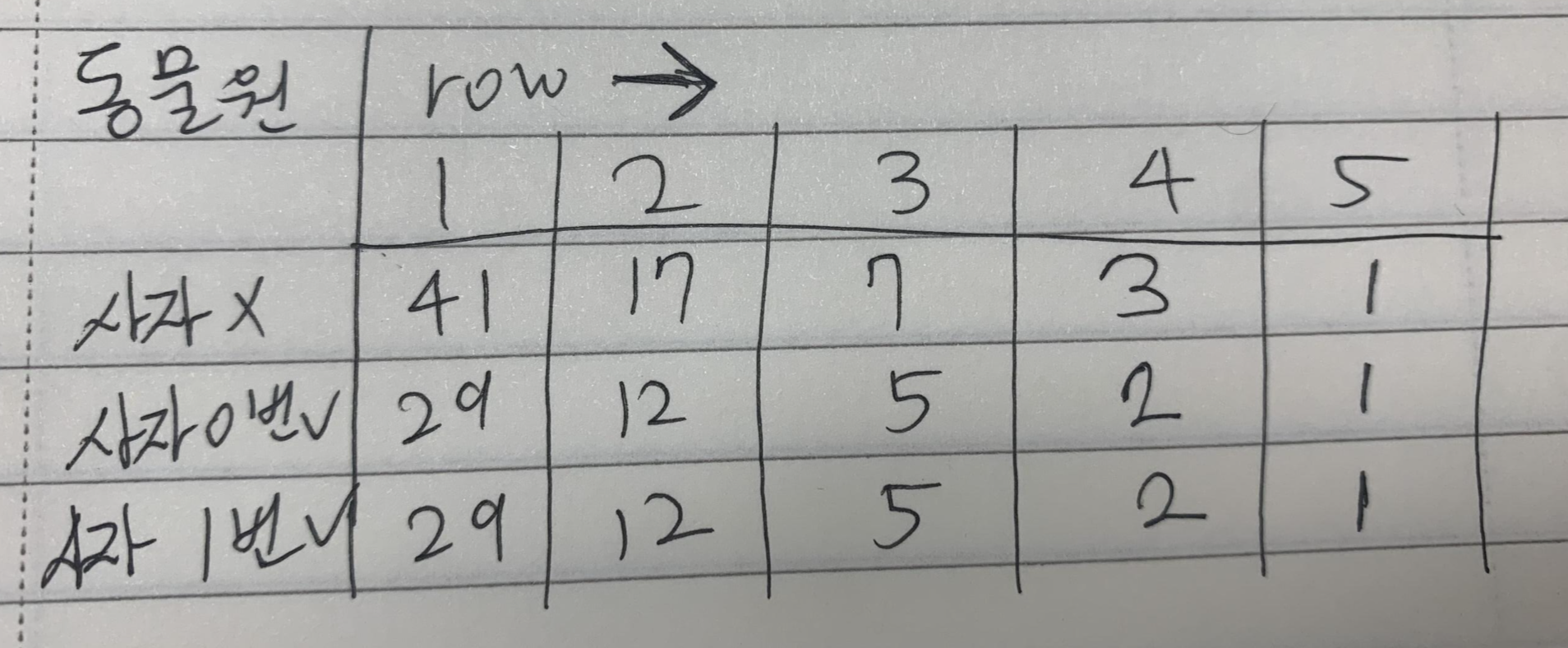
row행에서 사자를 놓는 모든 경우의 수 = row행에 사자를 놓지 않는 경우 + row행의 1번에만 사자를 놓는 경우 + row행의 2번에만 사자를 놓는 경우
row행에 사자를 놓지 않는 경우 = row+1행에 사자를 놓지 않는 경우 + row+1행의 1번에만 사자를 놓는 경우 + row+1행의 2번에만 사자를 놓는 경우
row행의 1번에만 사자를 놓는 경우 = row+1행에 사자를 놓지 않는 경우 + row+1행의 2번에만 사자를 놓는 경우
row행의 2번에만 사자를 놓는 경우 = row+1행에 사자를 놓지 않는 경우 + row+1행의 1번에만 사자를 놓는 경우
2. 코드
탑 다운 방식과 바텀 업 방식을 모두 사용해보았다
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
|
#include <iostream>
#include <cstring>
using namespace std;
int N, dp[100001][3];
int top_down(int row, int cage){
if(row == N-1) return 1;
int &ret = dp[row][cage];
if(ret != -1) return ret;
ret = 0;
switch(cage){
case 0:
ret += (top_down(row+1, 0) + top_down(row+1, 1) + top_down(row+1, 2))%9901;
break;
case 1:
ret += (top_down(row+1, 0) + top_down(row+1, 2))%9901;
break;
case 2:
ret += (top_down(row+1, 0) + top_down(row+1, 1))%9901;
break;
default: break;
}
return ret % 9901;
}
void bottom_up(){
dp[1][0] = 1;
dp[1][1] = 1;
dp[1][2] = 1;
for(int i = 2; i <= N; i++){
dp[i][0] = (dp[i-1][0] + dp[i-1][1] + dp[i-1][2])%9901;
dp[i][1] = (dp[i-1][0] + dp[i-1][2])%9901;
dp[i][2] = (dp[i-1][0] + dp[i-1][1])%9901;
}
cout << (dp[N][0] + dp[N][1] + dp[N][2])%9901;
}
int main(){
cin >> N;
// memset(dp, -1, sizeof(dp));
// cout << (top_down(0, 0) + top_down(0, 1) + top_down(0, 2))%9901;
bottom_up();
return 0;
}
|
cs |
'Algorithm > BOJ' 카테고리의 다른 글
| [백준 2143] 두 배열의 합 C++ (2) | 2021.05.30 |
|---|---|
| [백준 16929] Two Dots C++ (2) | 2021.05.27 |
| [백준 17298 17299] 오큰수 , 오등큰수 C++ (0) | 2021.05.25 |
| [백준 1644] 소수의 연속합 C++ (0) | 2021.05.24 |
| [백준 1300] K 번째 수 C++ (0) | 2021.05.23 |
![[백준 1309] 동물원 C++](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FbztVXC%2Fbtq5RCzkLcw%2FNZJ9bnQgThKTu5Sp47Ex30%2Fimg.png)