덧셈
덧셈을 수행하는 하드웨어를 병렬 가산기라고 부른다. 병렬 가산기는 비트 수만큼의 전가산기들로 구성된다.
반가산기
1비트 2진수 2개를 더한 합과 올림수를 구하는 하드웨어
1 + 1 => 결과값 1과 올림수 1을 출력한다.
전가산기
1비트 2진수 2개와 이전 단게의 올림수 1개, 총 3개의 이진수를 더하여 합과 올림수를 구하는 하드웨어
이전에 올라온 비트 1 + (0 + 1) 현재 위치의 비트 => 결과값 1과 올림수 1을 출력한다.
전가산기는 올림수 비트를 전송하는 선에 의해 서로 연결된다. 따라서 많은 비트를 연산하기 위해서 같은 방법으로 전가산기들을 계속 연결해 구성할 수 있다.
병렬 가산기

상태 레지스터
V : 오버플로우(oVerflow) 비트 (1인경우 오버플로우가 발생했다는 뜻이다)
Z : 영(Zero) 비트(결과 값이 0인 경우 1이 된다)
S : 부호(Sign) 비트(양수이면 0, 음수이면 1이 된다)
C : 올림수(Carry) 비트
0110 + 0011을 계산해 보자 (6 + 3) = 9

계산한 결과는 1001으로 -7이 된다.
이때 비트가 부족해서 오버플로우가 난걸 어떻게 확인하는지 알아보자.
마지막 비트의 올림수와 그 전 비트의 올림수를 XOR 연산해주면 오버플로우가 발생했는지 알 수 있다.
어떻게 XOR을 통해서 오버플로우를 감지할 수 있을까?
일단 음수와 양수의 덧셈같은 경우에는 오버플로우가 발생할 수 없는 구조이다.
그런데 음수 + 음수, 양수 + 양수 같은 경우에는 부호 비트가 변했는지를 확인하면 오버플로우를 감지할 수 있기 때문에 마지막 비트의 올림수와 그 전 비트의 올림수의 XOR 연산을 통해서 부호가 변했는지 확인할 수 있다.
뺄셈
빼고자 하는 숫자를 보수기에 통과시켜 음수로 변환시킨 후 가산기를 통해 계산한다.
보수기 연산 = ~A + 1
0011 => 1101
부호없는 2진수 곱셈
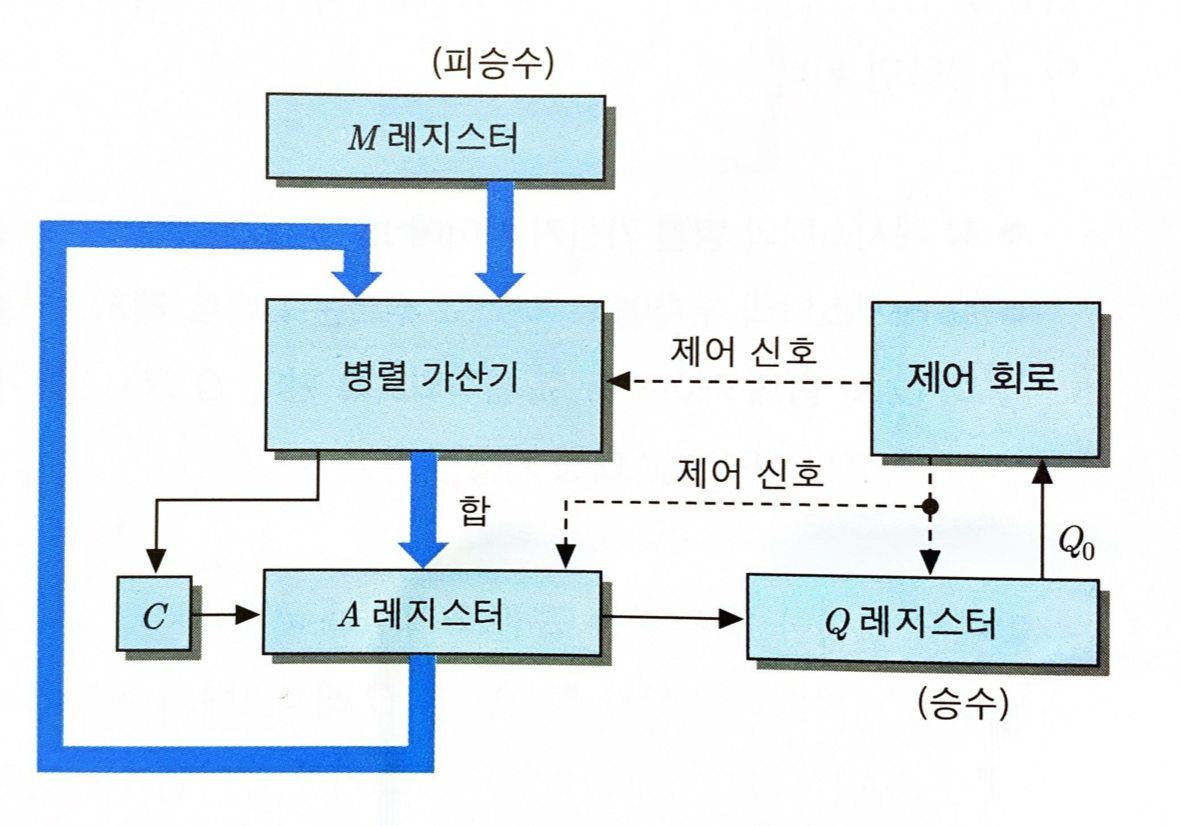
1101 * 1011 (13 * 11)
| C | A | Q | M | 동작 | |
| 초기 | 0 | 0000 | 1011 | 1101 | |
| 사이클 1 | 0 | 1101 | 1011 | 1101 | Q0가 1이므로 A <- A + M |
| 0 | 0110 | 1101 | 1101 | A, Q 레지스터 Right Shift | |
| 사이클 2 | 1 | 0011 | 1101 | 1101 | Q0가 1이므로 A <- A + M |
| 0 | 1001 | 1110 | 1101 | A, Q 레지스터 Right Shift | |
| 사이클 3 | 0 | 0100 | 1111 | 1101 | Q0가 0이므로 'A, Q 레지스터 Right Shift' 만 수행한다. |
| 사이클 4 | 1 | 0001 | 1111 | 1101 | Q0가 1이므로 A <- A + M |
| 0 | 1000 | 1111 | 1101 | A, Q 레지스터 Right Shift |
result : 1000 1111 (143)
부호 있는 2진수 곱셈
2의 보수들 간의 곱셈은 특별한 알고리즘이 개발되었다. 그 중에서 Booth 알고리즘을 사용해 곱셈을 하는 과정을 알아보자
1001 * 0011 (-7 * 3)
| A | Q | Q-1 | N | M | 동작 | |
| 초기 | 0000 | 0011 | 0 | 4 | 1001 | |
| 사이클 1 | 0111 | 0011 | 0 | 4 | 1001 | Q0 Q-1이 10이므로 A <- A - M 을 수행한다. |
| 0011 | 1001 | 1 | 3 | 1001 | Arithmetic Right Shift를 수행하고 계수에서 1을 뺀다. | |
| 사이클 2 | 0001 | 1100 | 1 | 2 | 1001 | Q0 Q-1이 11이므로 Arithmetic Right Shift와 계수-1만 수행한다. |
| 사이클 3 | 1010 | 1100 | 0 | 2 | 1001 | Q0 Q-1이 01이므로 A <- A + M 을 수행한다. |
| 1101 | 0110 | 0 | 1 | 1001 | Arithmetic Right Shift를 수행하고 계수에서 1을 뺀다. | |
| 사이클 4 | 1110 | 1011 | 0 | 0 | 1001 | Q0 Q-1이 00이므로 Arithmetic Right Shift와 계수-1만 수행한다. |
result: 1110 1011 (-21)
부호 없는 2진수 나눗셈
A ÷ B = q ... r
위 식에서 A는 나누어지는 수인 피제수(dividend)이고, B는 나누는 수인 제수(divisor)이다. 그리고 q과 r은 각각 몫(quotient)과 나머지 수(remainder)를 나타낸다.
위 그림은 피제수 10010011을 제수 1011로 나누는 과정을 보여준다. 먼저, 피제수의 비트틀을 좌측에서부터 우측으로 차례대로 검사하여, 제수가 피제수를 나눌 수 있게 될때까지 한 비트씩 이동하면서 검사를 반복한다.
부호 있는 2진수 나눗셈
0111 ÷ 1101 (7/(-3))
| A | Q | M | 동작 | |
| 초기 | 0000 | 0111 | 1101 | |
| 사이클 1 | 0000 | 1110 | 1101 | A, Q 레지스터 Left Shift |
| 1101 | 1110 | 1101 | A와 M의 부호가 다르므로 A <- A + M | |
| 0000 | 1110 | 1101 | A의 부호가 바뀌었으므로(연산 실패), Q0를 0으로 세팅하고 A값 복구 | |
| 사이클 2 | 0001 | 1100 | 1101 | A, Q 레지스터 Left Shift |
| 1110 | 1100 | 1101 | A와 M의 부호가 다르므로 A <- A + M | |
| 0001 | 1100 | 1101 | A의 부호가 바뀌었으므로(연산 실패), Q0를 0으로 세팅하고 A값 복구 | |
| 사이클 3 | 0011 | 1000 | 1101 | A, Q 레지스터 Left Shift |
| 0000 | 1000 | 1101 | A와 M의 부호가 다르므로 A <- A + M | |
| 0000 | 1001 | 1101 | A=0이므로(연산 성공), Q0 를 1로 세팅 | |
| 사이클 4 | 0001 | 0010 | 1101 | A, Q 레지스터 Left Shift |
| 1110 | 0010 | 1101 | A와 M의 부호가 다르므로 A <- A + M | |
| 1110 | 0010 | 1101 | A의 부호가 바뀌었으므로(연산 실패), Q0를 0으로 세팅하고 A값 복구 |
몫은 Q레지스터의 비트에 대한 2의 보수인 1110 (-2)
나머지는 A레지스터인 0001 (1)
'CS > Computer Architecture' 카테고리의 다른 글
| [컴퓨터 구조] 기억 장치 기본 (0) | 2021.12.29 |
|---|---|
| [컴퓨터 구조] 제어 유니트 (Control Unit) (0) | 2021.12.26 |
| [컴퓨터 구조] 산술 연산 (Shift) (2) | 2021.12.01 |
| [컴퓨터 구조] 컴퓨터 시스템 개요 (2) | 2021.11.24 |
| [컴퓨터 구조] Addressing Mode (0) | 2021.06.12 |
![[컴퓨터 구조] 산술 연산(덧셈, 곱셈)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FcqLZYC%2FbtrmKhM7jIm%2Fydsni5jizDhNMuPSWyPrBK%2Fimg.png)